Momen Gaya / Torsi
Pengertian Torsi
Perhatikan gambar di bawah
(gambar 1)
Gambar apakah di atas?
Good, pasti kamu sudah tahu ya. Itu adalah gambar pintu
Tahukah kamu mengapa gagang Pintu berada di bagian pinggir?
Ya banyak sekali alasan yang mungkin, diantaranya adalah :
1. Karena karena tempat lubang kunci harus dekat dengan tiang pintu (efisiensi)
2. Karena harus dijauhkan dari poros pintu, dll
1. Karena karena tempat lubang kunci harus dekat dengan tiang pintu (efisiensi)
2. Karena harus dijauhkan dari poros pintu, dll
Nah kalo kita lihat alasan yang kedua kita jadi bingung
kenapa harus jauh dari porosnya ya?
Untuk menjawabnya mari kita buat analogi lainnya ya
Mari kita lihat gambar berikut
(gambar 2)
Gambar apakah diatas? (fokuskan ke pria berkaos putih dan
anak berkaos hitam)
Ya benar, mereka sedang bermain jungkat-jungkit. Tapi kita
lihat posisi pria sangat dekat dengan tiang poros dan anak sangat jauh. Mengapa?
Ya benar agar seimbang. Dengan cara memberikan jarak yang
dekat untuk benda yang lebih berat dan memberikan jarak yang jauh untuk benda
yang lebih ringan.
Namun hal apakah yang kita maksud seimbang ini?
Ya.. itu adalah Momen gaya (selanjutya kita sebut torsi)
Jadi apa itu torsi ya?
Perhatikan perkalian berikut
5 x 2 = 2 x 5
Apakah hasil dari kedua ruas sama?
Ya tentu
Angka pertama kita sebut besaran pertama dan angka yang kedua
kita sebut besaran kedua
5 x 2 artinya besaran pertamanya adalah 5 dan besaran
keduanya adalah 2
2 x 5 artinya besaran pertamanya adalah 2 dan besaran
keduanya adalah 5
Nah kalo kita lihat tadi gambar 2 (jungkat-jungkit) kita
bisa umpamakan berat pria 5 dan jaraknya 2 sedangkan berat anak 2 dan jaraknya
5 sehingga kalo kita kali sama-sama jadi 10
Dari sini kita simpulkan bahwa nilai torsi ini hasil kali
dari besaran gaya (berat Misalnya) dan dan lengan gaya (jarak dari benda ke
poros), sehingga kita bisa rumuskan menjadi :
(rumus
1)
Nah kenapa lambangnya “x” bukan titik. Karena
torsi merupakan besaran vektor yang dihasilkan dari dua besaran yang arahnya
saling tegak lurus (berada di dua sumbu yang berbeda pada diagram kartesius)
jadi kalo satu sumbu torsi yang dihasilkan adalah “Nol”
(gambar 4)
Nah seperti itu jugalah pintu. Poros di sebelah kiri maka
kita letakkan gagang pintu di sebelah kanan tempat kita memberikan gaya untuk
mendorong pintu. Dengan dijauhkan maka akan terbentuk lengan gaya yang besar
sehingga kita hanya butuh gaya yang lebih sedikit untuk mendorong pintu. Karena
F ( gaya ) berbanding terbalik dengan r (lengan gaya)
(rumus
2)
Dikarenakan torsi merupakan vektor, maka
untuk lebih mudahnya jika putarannya searah jarum jam kita beri tanda “+”
(positif) dan jika berputar berlawanan arah jarum jam kita beri tanda “-“ (negatif)
Menentukan Arah Putaran Torsi
Bagaimana cara mudahnya menentukan arah
dari putarannya?
contoh:
Untuk lebih mudahnya kita bisa gunakan
pulpen kita agar lebih konkret (nyata)
Torsi Pada Gaya Yang Tidak Tegak Lurus
Tetapi
bagaimana jika gaya yang kita berikan tidak tegak lurus ?
Seperti gambar berikut :
(gambar
5)
Mari kita tinjau dahulu segitiga di bawah
ini
(gambar 6)
Karena sudut dalam bersebrangan maka sudut α bisa
masuk ke dalam segitiga dibagian kiri bawah
Maka Y = F sin α dan X = F cos α
Nah dalam hal ini jika kita perhatikan gambar 5 ada garis Y yang mengarah keatas (warna abu-abu) itu lah
gaya yang ingin kita pakai untuk mencari torsi
Sehingga :
Karena Y = F sin α , maka
atau
(rumus
3)
Torsi Total
Dan jika ada dua gaya atau lebih maka akan menghasilkan dua
torsi atau lebih sehingga torsi totalnya adalah
(rumus
4)
Bagaimana bisa dimengeti kah?
Insya Allah bisa ya
Contoh Soal
Sekarang kita coba beberapa contoh ya:
1.
Carilai besar momen gaya dari gambar berikut
ini!
Diketahui :
F = 20 N
r = 2 m
Dit : τ
= ?
Jawab
: τ = - F x r = - 20 x 2 = - 40 Nm (berlawanan arah jarum jam)
2.
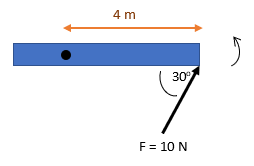
Carilai besar momen gaya dari gambar berikut
ini!
Diketahui :
F = 10 N
r
= 4 m
α = 30o
Dit : τ
= ?
Jawab
: τ = - F x r sin α = - 10 x 4 . 0,5 = - 20 Nm (berlawanan arah jarum jam)
3.
Carilai besar momen gaya dari gambar berikut
ini!
Diketahui
:
F1 = 50 N
F2 = 10 N
r1 = 1 m
r2 = 3 m
α2 = 30o
Dit : τ
= ?
Jawab : τ1 = F1
x r1 = 50 x 1 = 50 Nm (searah arah jarum jam)
τ = - F2
x r2 sin α2 = - 10 x 3 . 0,5 = - 15 Nm (berlawanan arah
jarum jam)
τtotal
= τ1 + τ2 = 50 + (-15) = 35 Nm (searah arah jarum jam)
4.
Carilai besar momen gaya dari gambar berikut
ini!
Untuk lebih jelasnya kita harus jadikan gaya F menjadi vektor satuan FX
dan FY dan jaraknya r menjadi rX dan rY serpeti
gambar berikut:
Diketahui
:
F = 100 N
FX = F Sin 53o
FY = F Cos 53o
rX = ½ x 8 = 4 m
rY = ½ x 12 = 6 m
α = 53o
Dit : τ
= ?
Jawab : τX = FX
x rX Cos 53o = 100
x 4 . 0,6 = 24 Nm (searah arah jarum
jam)
ΤY
= - FY x rY sin 53o
= - 100 x 6 . 0,8 = - 48 Nm (berlawanan arah jarum jam)
τtotal
= τX + τY = 24 + (-48) = -24 Nm (berlawanan arah jarum
jam)
Sekian dulu untuk Pembahasan Dinamika Rotasi dan Kesetimbangan Benda Tegar Part 1