FISIKA SMABI: Listrik Statis

Listrik statis (electrostatic) membahas muatan listrik yang berada dalam keadaan diam (statis).

Sifat-sifat Muatan Listrik

Muatan listrik digolongkan menjadi dua jenis yaitu muatan listrik positif dan muatan listrik negatif.
Muatan listrik yang sejenis akan saling tolak-menolak dan muatan listrik yang tak sejenis tarik-menarik.

Contoh Interaksi Muatan-muatan Listrik

Ada empat buah muatan A, B, C, dan D. A menarik B, A menolak C, C menarik D, dan D bermuatan positif. Tentukan jenis muatan-muatan lainnya!

Jawab:

C menarik D berarti C berlawanan jenis dengan D. Karen D bermuatan positif maka C bermuatan negatif. A menolak C berarti A sejenis dengan C. Karena C bermuatan negatif maka tentu A bermuatan negatif. A menarik B berarti A berlawanan jenis dengan B. Karena A bermuatan negatif maka tentu B bermuatan positif.

Formulasi Hukum Coulomb

Besar gaya tarik atau gaya tolak antara dua muatan listrik sebanding dengan muatan-muatannya dan berbanding terbalik dengan kuadrat jarak antara kedua muatan.

Secara matematis hukum Coulomb dinyatakan sebagai berikut:

$F=k\frac{q_{1}.q_{2}}{r^{2}}$

Dimana :

F = gaya tolak atau gaya tarik antara kedua muatan (N)

k = tetapan / konstanta = 9 x 109 Nm2C-2 untuk benda yang berada di dalam medium vakum (udara) dimana k = dan εo = 8,85 x 10-12C2N-1m2

q = besar muatan (C, dimana 1 μC = 10-6 C dan 1 nC = 10-9 C)

r = jarak antara kedua muatan (m)

Menggambar Vektor Gaya Coulomb

Ada dua hal yang perlu diperhatikan dalam menggambar vektor gaya Coulomb yaitu:

muatan sejenis tolak-menolak, muatan tak sejenis tarik-menarik.
vektor gaya Coulomb F terletak pada garis hubung kedua muatan.

Perhatikan gambar di bawah ini:

Gaya Coulomb dalam Bahan

Bila medium muatan bukan vakum atau udara maka besar gaya Coulomb antara muatan berkurang (Fbahan < Fudara). Jika medium memiliki permitivitas relatif εr (dahulu disebut tetapan dielektrik K), maka tetapan εo harus diganti dengan permitivitas bahan εyang dirumuskan dengan:

ε = εr εo

Sehingga gaya Coulomb dalam bahan dirumuskan dengan:

$F_{bahan}=\frac{1}{4\pi \varepsilon}\frac{q_{1}q_{2}}{r^{2}}$
Atau
$F_{bahan}=\frac{1}{4\pi \varepsilon_{r}\varepsilon _{0}}\frac{q_{1}q_{2}}{r^{2}}$
$F_{bahan}=\frac{1}{\varepsilon_{r}4\pi \varepsilon _{0}}\frac{q_{1}q_{2}}{r^{2}}=\frac{1}{\varepsilon _{r}}.\frac{1}{4\pi \varepsilon _{0}}.\frac{q_{1}q_{2}}{r^{2}}$
$F_{bahan}=\frac{1}{\varepsilon _{r}}.F_{Vakum}$
Contoh Soal dan Penyelesaian

Dua buah muatan masing-masing 20 μC dan 24 μC terpisah pada jarak 12 cm. Hitung besar gaya yang bekerja pada kedua muatan tersebut bila:

a. kedua muatan diletakkan di udara

b. kedua muatan diletakkan dalam bahan yang memiliki permitivitas relatif 3.

Penyelesaian:

Dik:

q1 = 20 μC = 20 x 10-6 C

q2 = 24 μC = 24 x 10-6 C

r = 12 cm = 12 x 10-2 m

k = 9 x 109 Nm2C-2

εr = 3

Dit:

a. Fudara = …………..?

b. Fbahan = …………..?

Jawab:
di udara
$F=k.\frac{q_{1}q_{2}}{r^{2}}=9x10^{9}.\frac{20x10^{-6}.24x10^{-6}}{\left (12X10^{-2} \right )^{2}}=9x10^{9}.\frac{20x10^{-6}.24x10^{-6}}{144x10^{-4}}=30x10^{1}=300N$

di bahan
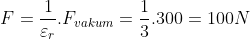
$F=\frac{1}{\varepsilon _{r}}.F_{vakum}=\frac{1}{3}.300=100N$

Resultan dua gaya Coulomb yang segaris

Sebuah partikel bermuatan +2 μC diletakkan pada garis hubung diantara partikel-partikel bermuatan -2 μC dan -4 μC yang berjarak 0,4 m. Tentukan besar gaya pada partikel bermuatan +2 μC jika diletakkan di tengah-tengah kedua partikel bermuatan negatif!

Penyelesaian:

Dik:

q1 = -2 μC = -2 x 10-6 C

q2 = -4 μC = -4 x 10-6 C

q3 = 2 μC = 2 x 10-6 C

k = 9 x 109 Nm2C-2

Dit:

F = ….? jika r31 = r32

Jawab:

Untuk r31 = r32 = a = 0,2 m

Arah ke kanan ditetapkan sebagai gaya positif maka:

F = F32 + (-F31)

$F_{31}=k\frac{q_{3}q_{1}}{r^{2}}$
$F_{31}=9x10^{9}\frac{2x10^{-6}.2x10^{-6}}{4x10^{-2}}$
$F_{31}=9x10^{-1}=0,9$

$F_{32}=k\frac{q_{3}q_{2}}{r_{32}}=9x10^{9}\frac{2x10^{-6}.4x10^{-6}}{0,2^{2}}$
$F_{32}=9x10^{9}\frac{2x10^{-6}.4x10^{-6}}{4x10^{-2}}$
$F_{32}=18x10^{-1}=1,8$
$F=F_{32}+\left (-F_{31 \right )}=1,8-0,9=0,9N$
Tanda positif menyatakan bahwa arah resultan gaya pada q3 berarah ke kanan atau mendekati q2.

Catatan: Dalam perhitungan besar gaya Coulomb, tanda muatan tidak dimasukkan. Tanda muatan hanya digambarkan pada vektor gaya Coulomb, untuk menentukan gaya tolak atau gaya tarik.

Kuat Medan Listrik

Jika ada muatan q2 yang berada di sekitar muatan lain q1 maka muatan q2 akan merasakan gaya Coulomb dari q1. Daerah yang masih merasakan pengaruh gaya Coulomb ini dinamakan medan listrik. Medan listrik ini didefinisikan sebagai gaya yang dirasakan oleh muatan uji positif 1 C.
Dua hal yang perlu diperhatikan untuk menggambar vektor kuat medan listrik pada suatu titik adalah

1. vektor E menjauhi muatan sumber positif (gambar pertama) dan mendekati muatan sumber negatif (gambar kedua)

2. vektor E memiliki garis kerja sepanjang garis hubung antara muatan sumber dengan titik yang akan dilukis vektor kuat medannya.

Sedangkan besar medan listrik dinamakan kuat medan listrik dirumuskan seperti berikut.
$E=\frac{F}{q_{2}}=\left ( \frac{k\frac{q_{1}q_{2}}{r^{2}}}{q_{2}} \right )=k\frac{q_{1}}{r^{2}}$
dengan

F = Gaya Coulomb (N)

E = kuat medan listrik (N/C)

q = muatan listrik (coulomb)

r = jarak titik dari muatan (m)

k = 9 x 109 Nm2/C2

Contoh Soal dan Penyelesaian

1. Sebuah muatan uji +3 x 10-5 C diletakkan dalam suatu medan listrik. Gaya Coulomb yang bekerja pada muatan uji tersebut adalah 0,45 N. Berapa besar kuat medan listrik pada muatan uji?

Penyelesaian:

Dik:

qo = +3 x 10-5 C

F = 0,45 N

Dit: E = …. ?

Jawab:
$E=\frac{0,45}{3x10^{-5}}=0,15x10^{5}N/m$
Jadi besar kuat medan listriknya adalah $0,15x10^{5}N/m$

2. Tentukan kuat medan listrik dan arahnya pada jarak 1 cm dari sebuah muatan positif 10-6 C!

Penyelesaian:

Dik:
r = 1 cm = 1 . 10-2 m
q = 10-6 C

Dit: E = ….?

Jawab:
$E=k\frac{q}{r^{2}}=9x10^{9}\frac{10^{-6}}{10^{-2}}=9x10^{5}N/m$

Karena muatan sumber bermuatan positif maka medan listrik di titik tersebut menjauhi muatan sumber.

Hukum Gauss

Pengertian Garis-garis Gaya Listrik

Medan listrik dapat divisualkan dengan menggunakan garis-garis medan listrik (ada juga yang menyebutnya garis-garis gaya listrik).

Tiga hal tentang garis-garis medan listrik:

Garis-garis medan listrik tidak pernah berpotongan
Garis-garis medan listrik selalu mengarah radial ke luar menjauhi muatan positif dan radial ke dalam mendekati muatan negatif (lihat gambar di atas)
Tempat di mana garis-garis medan listrik rapat menyatakan tempat yang medan listriknya kuat. Sedangkan tempat dimana garis-garis medan listrik renggang menyatakan tempat yang medan listriknya lemah.

Formulasi Hukum Gauss

Teknik sederhana untuk menentukan kuat medan listrik bagi distribusi muatan kontinu dikembangkan oleh Karl Friedrich Gauss (1777 – 1855). Sebelum membahas tentang hukum ini lebih jauh, akan dibahas terlebih dahulu mengenai konsep fluks listrik.

Fluks listrik didefinisikan sebagai jumlah garis-garis medan listrik yang menembus tegak lurus suatu bidang (perhatikan gambar di atas). Secara matematis fluks listrik dirumuskan dengan:

Ф = E x A

Dimana:

Ф = fluks listrik (NC-1m2 atau disebut Weber)

E = kuat medan listrik (N/C)

A = luas bidang (m2)

Jika garis-garis medan listrik menembus suatu bidang dengan tidak tegak lurus maka fluks listrik dapat ditentukan dengan:

Ф = E A cos θ

Dengan θ adalah sudut yang dibentuk oleh garis medan listrik dengan garis normal bidang (n).

Contoh Soal dan Penyelesaian

Hitung jumlah garis medan yang menembus suatu bidang persegi panjang yang panjangnya 30 cm dan lebarnya 20 cm, bila kuat medan listrik homogen sebesar 200 N/C dan arahnya:

searah dengan bidang
membentuk sudut 30o terhadap bidang
tegak lurus terhadap bidang

Penyelesaian:

Dik:
p = 30 cm = 0,3 m

l = 20 cm = 0,2 m

E = 200 N/C

Dit: Ф = ….? (untuk tiga kondisi)

Jawab:

Hitung A terlebih dahulu:

A = p x l = 0,3 x 0,2 = 0,06 m2

1. Untuk arah kuat medan yang searah bidang berarti arah kuat medan tegak lurus dengan normal bidang ( = 90o). Dari persamaan (10) Ф = E A cos θ, karena cos 90o = 0 maka Ф = 0.

2. Untuk kuat medan listrik yang membentuk sudut 30o terhadap bidang dapat dilihat pada gambar berikut:

Ф = E A cos θ = 200 x 0,06 cos 60o = 200 x 0,06 x ½ = 6 Weber

3. Untuk kuat medan listrik yang tegak lurus bidang dapat dilihat pada gambar berikut:

Ф = E A cos θ = 200 x 0,06 cos 0o = 200 x 0,06 x 1 = 12 Weber

Dari konsep fluks listrik yang telah dibahas di atas inilah Gauss merumuskan hukumnya yang berbunyi:

Jumlah garis-garis medan listrik (fluks listrik) yang menembus suatu permukaan tertutup sama dengan jumlah muatan listrik yang dilingkupi oleh permukaan tertutup itu dibagi dengan permitivitas udara εo.

Secara matematis:

$\Phi =E.Acos\theta =\frac{\sum q}{\varepsilon _{0}}$

Dimana:

A = luas permukaan tertutup

θ = sudut antara E dengan arah normal n

∑q = muatan total yang dilingkupi oleh permukaan tertutup.

Potensila Listrik

Potensial listrik didefinisikan sebagai perubahan energi potensial per satuan muatan ketika sebuah muatan uji dipindahkan di antara dua titik atau secara matematis dirumuskan dengan:

$V=\frac{Ep}{q}$
$V=k\frac{q}{r}$

dengan

V = potensial listrik

Ep = Energi Potensial (Joule)

q=muatan listrik (C)

Dimana V = beda potensial dalam satuan SI dinyatakan dalam J/C dan diberi nama volt (disingkat V) untuk menghormati Alessandro Volta (1745 – 1827), seorang ilmuwan Italia yang menemukan baterai listrik.

Kapasitor

Kapasitor adalah suatu komponen elektronika yang terdiri atas dua keping bermuatan listrik yang sama besarnya, tetapi berlawanan jenisnya. Bentuk kapasitor bermacam-macam, diantaranya berbentuk keping sejajar, bola sepusat, dan bentuk silinder atau tabung.

Kegunaan Kapasitor

Kapasior digunakan untuk menghindari terjadinya loncatan listrik pada rangkaian-rangkaian yang mengandung kumparan bila tiba-tiba arus listrik diputuskan. Kapasitor dapat juga berfungsi sebagai penyimpan muatan atau energi listrik dan sebagai tunning untuk memilih panjang gelombang yang dikehendaki pada pesawat radio.

Kapasitas Kapasitor

Kapasitas adalah kemampuan menyimpan muatan. Sesuai dengan kegunaannya, kapasitas suatu kapasitor bergantung pada dimensi atau ukurannya dan medium-medium yang ada di dalam kapasitor tersebut. Makin besar ukuran suatu kapasitor, makin besar pula kemampuannya untuk menyimpan muatan listrik. Kapasitor mempunyai kapasitas C, yang dinyatakan sebagai perbandingan yang tetap antara muatan q dari salah satu penghantarnya terhadap beda potensial antara keping penghantar itu.
$C=\frac{q}{V}$
Sedangkan kapasitas kapasitor untuk keping sejajar akan menjadi:
$C=\varepsilon _{0}\frac{A}{d}$

Dimana:
C=kapasitas kapasitor (Farad)
$\varepsilon _{0}$ =permitivitas ruang hampa
A=luas tiap-tiap keping
d = jarak antar keping

Kapasitas kapasitor yang berbentuk bola dirumuskan dengan:

C = = 4πεoR

Dengan R adalah jari-jari bola.

Susunan Kapasitor

1. Kapasitor disusun seri

Dua kapasitor atau lebih bila disusun seri maka muatan pada tiap-tiap kapasitornya sama sebab muatan total seluruh kapasitor sama dengan muatan tiap-tiap kapasitor.

Untuk kapasitor yang disusun seri:

$V_{s}=V_{1}+V_{2}+V_{3}+V_{4}+....$
$q_{s}=q_{1}+q_{2}+q_{3}+q_{4}+....$
$\frac{1}{C_{s}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+.....+\frac{1}{C_{n}}$

2. Kapasitor disusun paralel
Apabila ada beberapa buah kapasitor dipasang paralel maka kapasitor-kapasitor tersebut akan mempunyai beda potensial yang sama, dan sama dengan beda potensial gabungan seluruh kapasitor.Sedangkan kapasitas gabungannya lebih besar dari kapasitas tiap-tiap kapasitor. Jadi, untuk mendapatkan kapasitas kapasitor yang besar, kapasitor-kapasitor harus disusun secara paralel.

Untuk kapasitor yang disusun paralel:

V = V1 = V2 = V3

q = q1 + q2 + q3+…..

Kapasitas kapasitor pengganti untuk kapasitor yang disusun secara paralel yaitu:

Cg = C1 + C2 + C3 +…….

Energi yang Tersimpan dalam Kapasitor

Bila sebuah kapasitor diberikan muatan listrik, sesungguhnya yang terjadi adalah perpindahan muatan dari satu keping ke keping yang lainnya. Untuk itu diperlukan usaha. Usaha yang telah dipakai untuk pemberian muatan itu akan disimpan oleh kapasitor sebagai energi. Secara matematis usaha tersebut dirumuskan sebagai:

$W=\frac{1}{2}\frac{q^{2}}{C}$
$W=\frac{1}{2}CV^{2}$

Contoh Soal dan Penyelesaian

1. Tentukan kapasitas kapasitor keping sejajar yang mempunyai luas keping 2 cm2 dan jarak antarkepingnya 0,4 cm , bila muatan tiap-tiap keping sebesar 10-6 μC dan εo = 8,85 x 10-12 C2/Nm2!

Penyelesaian:

Dik:

A = 2 cm2 = 2 x 10-4 m2

d = 0,4 cm = 4 x 10-3 m

q = 10-6 μC = 10-12 C

εo = 8,85 x 10-12 C2/Nm2

Dit: Cs = …. ?

Jawab:

$C=\varepsilon _{0}\frac{A}{d}=8,85x10^{-12}\frac{2x10^{-4}}{4x10^{-3}}=4,425x10^{-13}F$

2. Dua buah kapasitor masing-masing kapasitasnya 2 μF dan 3 μF dipasang secara seri. Beda potensial antara ujung-ujung gabungannya 10 volt. Tentukanlah:

a. kapasitas gabungannya

b. muatan tiap-tiap kapasitor

c. beda potensial tiap-tiap kapasitor

Penyelesaian:

Dik:

susunan seri → q sama di tiap-tiap kapasitor

C1 = 2 μF = 2 x 10-6 F

C2 = 3 μF = 3 x 10-6 F

Vg = 10 V

Dit:

a. Cg = …. ?

b. q1 = …. ? dan q2 = …. ?

c. V1 = …. ? dan V2 = …. ?

Jawab:

a. C gabungan
$\frac{1}{C_{s}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}$
$\frac{1}{C_{s}}=\frac{1}{2x10^{-6}}+\frac{1}{3x10^{-6}}$
$\frac{1}{C_{s}}=\frac{1x10^{6}}{2}+\frac{1x10^{6}}{3}$
$\frac{1}{C_{s}}=\left (\frac{1}{2}+\frac{1}{3} \right )x10^{6}$
$\frac{1}{C_{s}}=\left (\frac{3}{6}+\frac{2}{6} \right )x10^{6}$
$\frac{1}{C_{s}}=\left (\frac{5x10^{6}}{6} \right )$
$\frac{C_{s}}{1}=\left (\frac{6}{5x10^{6}} \right )$
$C_{s}=1,2x10^{-6}$

Cg = = 1,2 μF = 1,2 x 10-6 F

b. muatan tiap-tiap kapasitor
$C_{g}=\frac{q_{g}}{V_{g}}$
$q_{g}=C_{g}V_{g}=\left ( 1,2x10^{-6} \right ).10=12x10^{-6}C$

c. beda potensial tiap kapasitor
$V_{1}=\frac{q_{1}}{C_{1}}$
$V_{1}=\frac{12x10^{-6}}{2x10^{-6}}=6V$

$V_{2}=\frac{q_{2}}{C_{2}}$
$V_{2}=\frac{12x10^{-6}}{3x10^{-6}}=4V$

3. Dua buah kapasitor dipasang secara seri dengan kapasitas masing-masing 1 μF dan 2 μF dan beda potensial antara ujung-ujungnya 6 volt. Tentukanlah energi yang tersimpan pada tiap-tiap kapasitor!

Penyelesaian:

Dik: susunan seri → q sama di tiap-tiap kapasitor

C1 = 1 μF = 1 x 10-6 F

C2 = 2 μF = 2 x 10-6 F

Vg = 6 V

Dit: W1 = …. ? dan W2 = …. ?

Jawab:

$w=\frac{1}{2}\frac{q_{1}^{2}}{C_{1}}\Rightarrow hitung dulu besarnya q$
$\frac{1}{C_{g}}=\frac{1}{C_{1}}+\frac{1}{C2}=\frac{1}{1}+\frac{1}{2}=\frac{2}{2}+\frac{1}{2}=\frac{3}{2}$
$\frac{C_{g}}{1}=\frac{2}{3}$
$C_{g}=\frac{2}{3}x10^{-6}F$
$q_{g}=C_{g}V_{g}=\frac{2}{3}x10^{-6}.6=4x10^{-6}C$
$w_{1}=\frac{1}{2}\frac{q_{g}^{2}}{C_{1}}=\frac{1}{2}\frac{\left (4x10^{-6} \right )^{2}}{1x10^{-6}}=8x10^{-6}J$
$w_{2}=\frac{1}{2}\frac{q_{g}^{2}}{C_{2}}=\frac{1}{2}\frac{\left (4x10^{-6} \right )^{2}}{2x10^{-6}}=4x10^{-6}J$

Soal dan Pembahasan

Sahabat fisoontal, untuk lebih memahami materi fisika serta untuk mempersiapkan diri untuk menghadapi UAS, UN, SBMPTN, berikut akan diberikan contoh soal beserta tips dan trik pembahasannya. Bagaimana sudah siap? Ayo kita mulai!

Materi: Listrik Statis

Sumber : https://fisikakontekstual.com/materi-lstrik-statishttpswww-nusapenidatourism-com/

FISIKA SMABI

Rabu, 24 Juni 2020

Listrik Statis

VEKTOR

Laporkan Penyalahgunaan

Label